Modules¶
circuits.py: Circuit synthesis module¶
This module is used for constructing filters from the transfer function specifications. It is intended for use with mrfilter, but can be used standalone.
Note
This file documents only those functions and methods with complicated math. Its purpose is to make verification of the math easy. Most equations reference one of the sources, but for some the full derivation is given. For general API documentation, import the module and study the docstrings.
- circuits.pbgain(Z, P, k)¶
Returns the passband gain of the given transfer func in ZPk format
For a filter with z zeros and p poles, the transfer function in [b, a] format will be
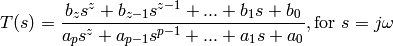
For low-pass filters, the passband gain will be
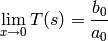
For high-pass filters, the passband gain will be
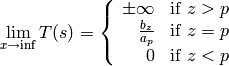
Todo
passband gain for band-pass, band-stop, all-pass
- class circuits.Biquad(Z, P, k)¶
General representation of a filter with a biquadratic transfer function
- synth_q()¶
Calculate the q from synthesized component values
Relevant equations:
- low-pass: [1], eq 6.56
- band-pass: [1], eq 7.30
- high-pass: TODO: check the TI app note
- band-stop: [1], eq 12.33
In all cases, the
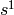 term of the denominator equals
term of the denominator equals
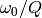
- synth_w0()¶
Calculate the w0 from synthesized component values.
The equations are the same as for synth_q
In all cases, the
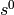 term of the denominator equals
term of the denominator equals
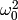
- class circuits.Cascade(approx, topology)¶
Represent a cascade connection of multiple filters
- class circuits.OnePole(Z, P, k)¶
One pole R-C filter
- get_sens(property, refdes)¶
Return the Bode sensitvity of property wrt refdes.
Supported properties: ѡ0, h
ѡ0 and h are identically defined for low-pass and high-pass filters. So their sensitivities are also identical.
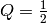 ,
from [1], eq. 5.9 .
,
from [1], eq. 5.9 .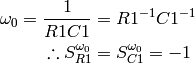
Using eq 9.32 from [1]:
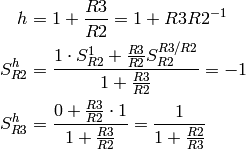
- synth_tf()¶
Return the transfer function of the entire cascade from calculated component values.
Low pass case from [1], eq. 3.3
- _synthesize()¶
Perform the circuit synthesis.
The equations to satisfy are:
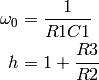
- class circuits.SallenKey(Z, P, k)¶
Generalized Sallen-Key filter, without resistive gain enhancement
- get_sens(property, refdes)¶
Return the Bode sensitvity of property wrt refdes.
Supported properties: w0, q, h.
For low-pass filters, the equations are from [1], pp 269-270. However, note that eq. 9.58 contains an error. The correct equation is
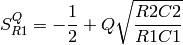
The high-pass SallenKey transfer function is (from page 67 of my notebook)
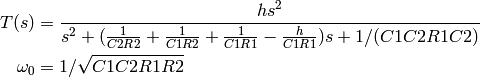
So
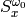 is the same as for low-pass filters, for all
is the same as for low-pass filters, for all
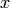 . Similarly,
. Similarly, 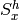 is the same for all shapes of SallenKey
filter. To find the sensitivities of
is the same for all shapes of SallenKey
filter. To find the sensitivities of 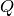 , we use the same strategy
as used in §9.2 of [1].
, we use the same strategy
as used in §9.2 of [1].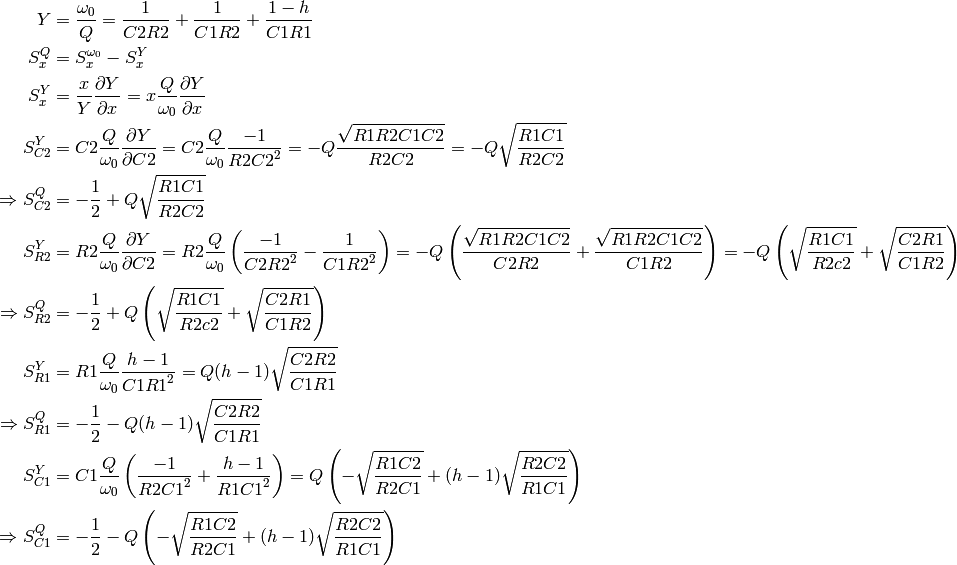
To find the sensitivities of
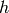 , first rewrite
, first rewrite 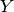 in terms
of R3 and R4.
in terms
of R3 and R4.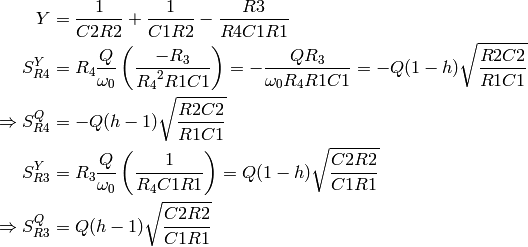
Todo
Derive sensitivities for bandpass, bandstop, and allpass
- synth_tf()¶
Calculate the transfer function from synthesize component values.
The low-pass case is given in [1] eq 6.55 . The high-pass case is given in [3], eq 11. Note that [3] uses a different convention for resistor numbering than is used in this program. Rearranging eq 11 gives the transfer function as used here:
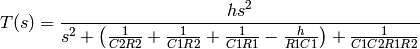
Todo
band-pass, band-stop, and allpass
- _synthesize()¶
Perform the componenet value calculations.
Strategy is from [3]:
- try simplification 4 (
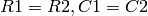 )
) - if that fails, try simplification 3 (
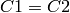 )
) - if that fails, try simplification 1, the most general case
Simplification 2 is not used here because it is just a special case of simplification 1.
- try simplification 4 (
- _simplification4(w0, q, h)¶
Attempt to synthesize using simplification 4 from SLOA024B.
Simplification 4 sets
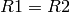 and
and 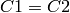
- _simplification3(w0, q, h)¶
Attempt to synthesize using simplification 3 from SLOA024B.
Simplification 3 sets C1=C2 and R2 = m*R1
- _simplification1(w0, q, h)¶
Attempt to synthesize using simplification 1 from SLOA024B.
Simplification 1 is the most general. It sets R2=m*R1 and C2=n*C1
| [1] | (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11) M. E. VanValkenburg, Analog Filter Design. New York, 1982 |
| [2] | Alan V. Oppenheim, Alan S. Willsky, S. Hamid Nawab, Signals & Systems 2nd edition. New Jersey, 1983 |
| [3] | (1, 2, 3) Texas Instruments, “Analysis of the Sallen-Key Architecture (Rev. B)” , Texas Instruments, SLOA024B, September 2002. [Online]. Available: http://focus.ti.com/general/docs/litabsmultiplefilelist.tsp?literatureNumber=sloa024b . [Accessed: May, 2009]. |